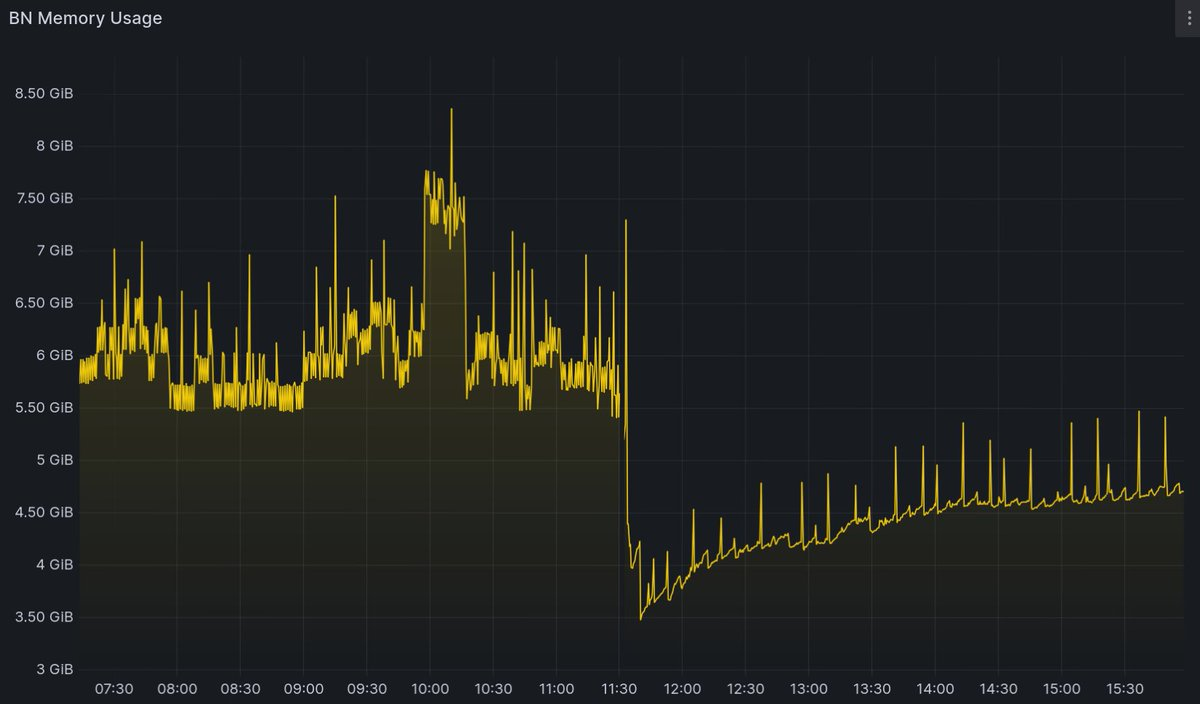
Lighthouse v5.2.0 release includes a complete rework of how it handles the BeaconState data structure, which is at the core of Ethereum's consensus layer. The BeaconState includes validator data like activation time, balances, etc. Unlike the execution layer's state which is 50GB+, the beacon state is small enough to fit entirely in memory. Because of the massive success of the beacon chain, the state has grown from 5 MB at genesis to 150 MB today. Laid out in memory with caches for quick access, states end up being larger, 500MB+ on mainnet, or 1GB on the Holesky testnet.
The problem is, we don't just need 1 state, we need several states at different points in time — at the head, at the justified checkpoint, at finalization, and so on. When there's a reorg, we need to wind back and get the pre-state which is usually just 1 slot behind the head. When we receive a block from the network with an old parent we have to again load and re-compute and old state. Here lies the trade-off: we want to process everything as quickly as possible (have more states in memory), but at the same time limit memory usage by Lighthouse (have fewer states in memory). The fundamental issue is that we must pay 500 MB of RAM for every state, but can we do better?
You see, beacon states happen to be mutated very sparsely. We can use this fact to our advantage and represent states in a way that de-duplicates data such that each additional state costs much less than 500 MB of RAM. That way we can have our cake and eat it too: lots of states, faster processing, and bounded memory usage.
To visualize how to store mutations differentially, consider a base state that holds all the data (green state). Then descendant states include a pointer to their base state plus their collection of mutations (yellow state).
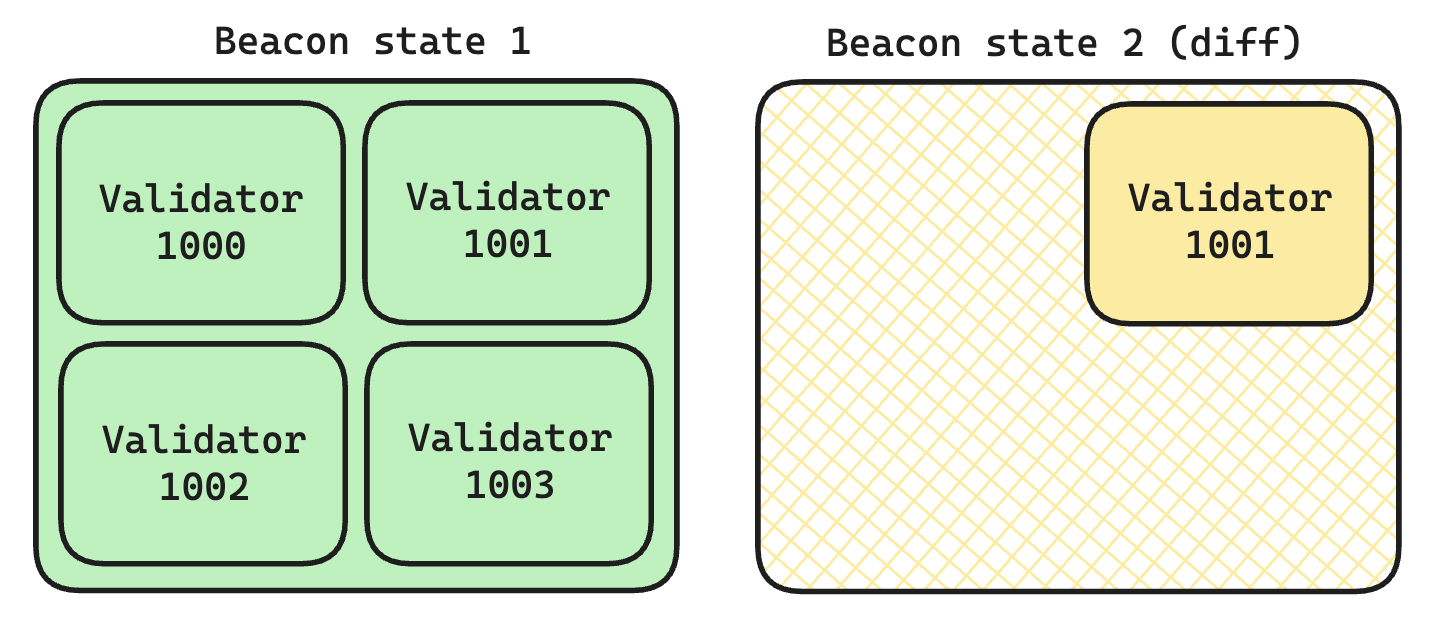
This approach is valid, and Lighthouse will use it for its new database scheme (TBA). However, there's a more elegant approach using persistent data structures from functional programming, making use of a property called structural sharing.
Instead of representing the BeaconState as a flat piece of memory, we lay out its data as a binary merkle tree. Any intermediary node inside the tree can point to another state's data, achieving massive de-duplication.
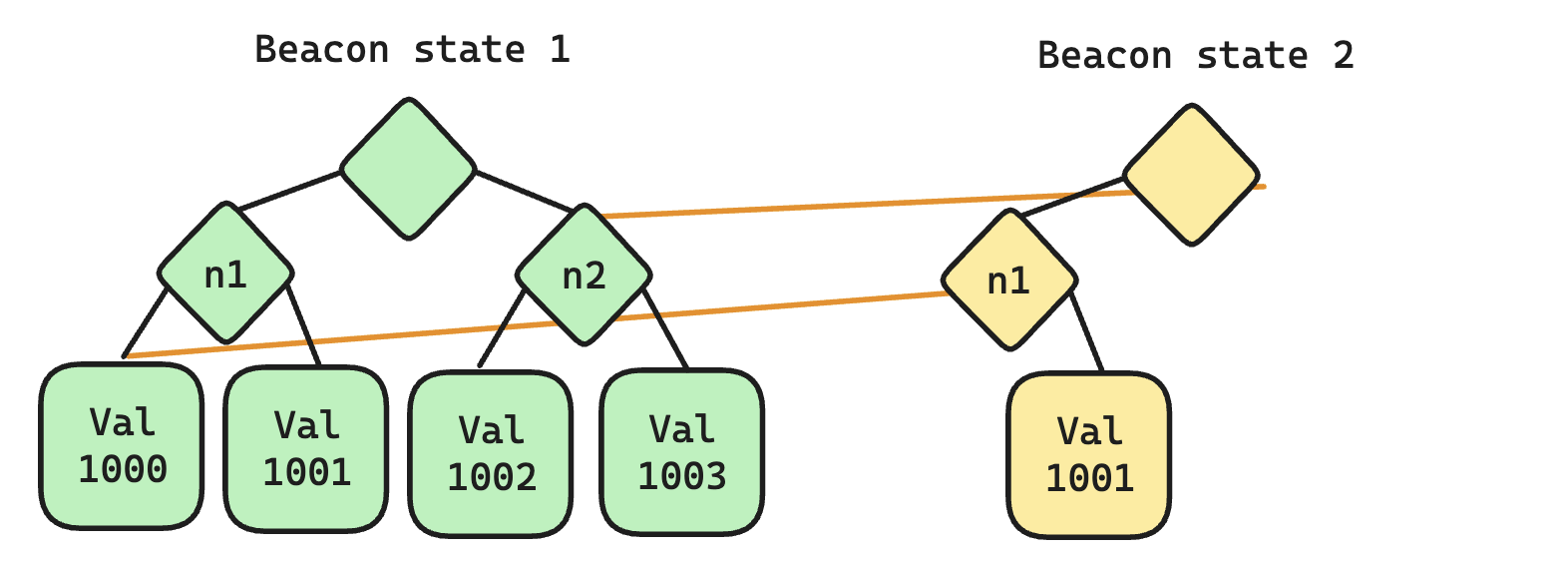
This is perfect for the blockchain paradigm, where we have a tree of blocks descended from the latest finalized block, and allow fork choice to choose the best tip amongst them. It also works nicely to speed up state hashing. After processing every beacon block we must hash the BeaconState, as a binary merkle tree. With tree states, we have already constructed this binary merkle tree, by design! To not have to hash the same data over and over, we attach hashes to each intermediary node. And thanks to its structural sharing nature, these cached values are re-used by all descendant states.
Now, we can keep almost all of these states in memory, which means Lighthouse can jump back to any unfinalized state nearly instantly. We still need to use heuristics to drop states if finalization lapses, but for 99% of the time when finality is regular, we can cruise along with every state in memory. You can hopefully see how this makes reorgs faster to process. Instead of doing a bunch of copying, or cache missing, we can just grab the previous state straight from memory and apply the new block to it. Regular blocks are also quicker to produce and process because we can skip the expensive copying step required to retain the previous state. Copying went from O(n) to O(1)!
Let's dive into the details of how tree-states are built.
Milhouse
This library implements a persistent binary merkle tree, with some tricks to batch and speed up mutations. Note that it only implements arrays (Vector and List), as Containers are much smaller and won't benefit from structural sharing.
The name is a homage to Milhouse Van Houten, who we must assume knows a thing or two about trees given his name – Houten being Dutch for "wooden". Dutch is also the native language of the inimitable Protolambda whose remerkleable library was a great inspiration.
The main caveat of tree-states and persistent data structures is that reading from large arrays becomes more expensive. Let's compare random access of some index. On a regular array, you can just jump directly to the location of the item.
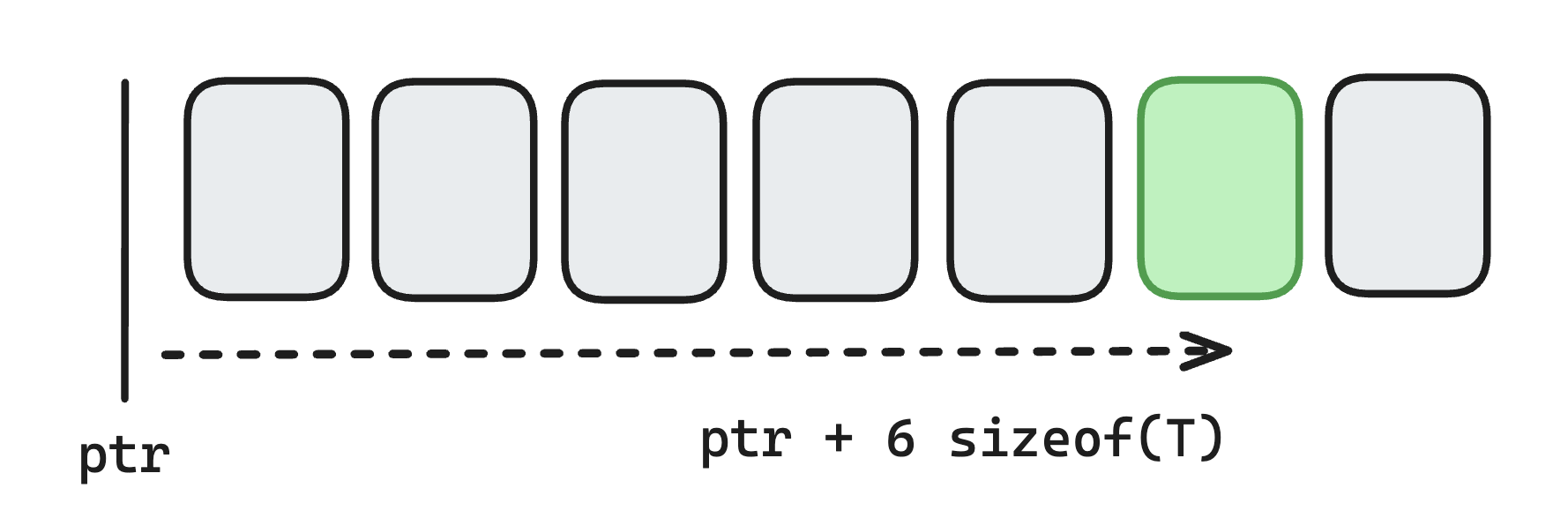
However, on a binary merkle tree you must traverse multiple pointers (which may not be contiguous in memory) to reach a specific item.
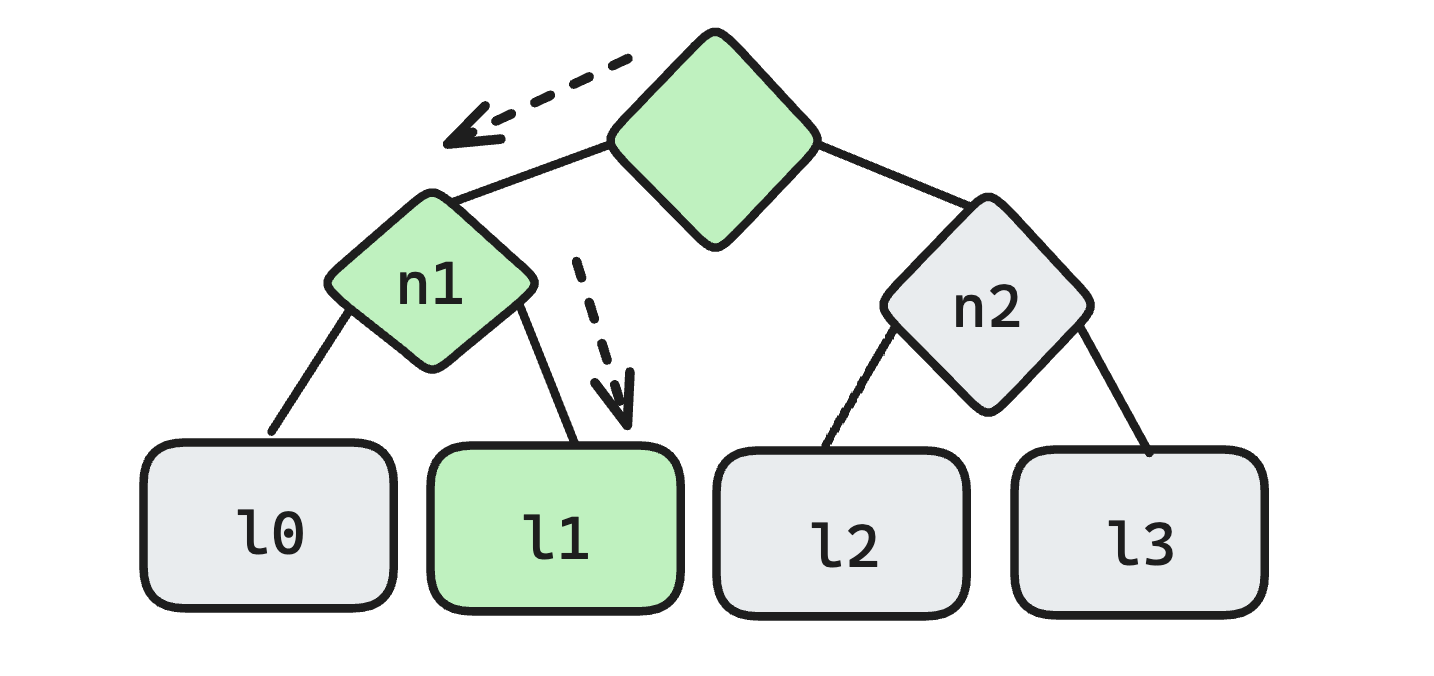
Iteration is also more expensive for the same reason. Therefore, most of the complexity in the Milhouse library is meant to optimize the costs of working with large trees.
| Operation | Linear array | Binary merkle tree |
|---|---|---|
| Random access | O(1) | O(log(n)) |
| Iteration | O(n) | O(n) |
Here \(n\) is the number of items stored in the array. Although iteration has the same Big-O time complexity (we iterate ~2n nodes total), the constant factor is substantially larger due to pointer chasing.
If you like algorithmic optimizations, the next sections are for you. Let's look at a couple of examples of strategies to minimize tree traversals on expensive operations.
Batch apply updates
When modifying our persistent binary merkle tree, we need to create and re-bind log(n) intermediate nodes for each leaf. During the execution of a beacon block, many individual nodes are modified. Instead of having to re-bind all those log(n) nodes every time, we create a temporary layer of pending updates. In a way, we overlay a diff on top of our tree. Then, after completing execution we apply those updates all at once, minimizing the total count of tree traversals and re-bindings.
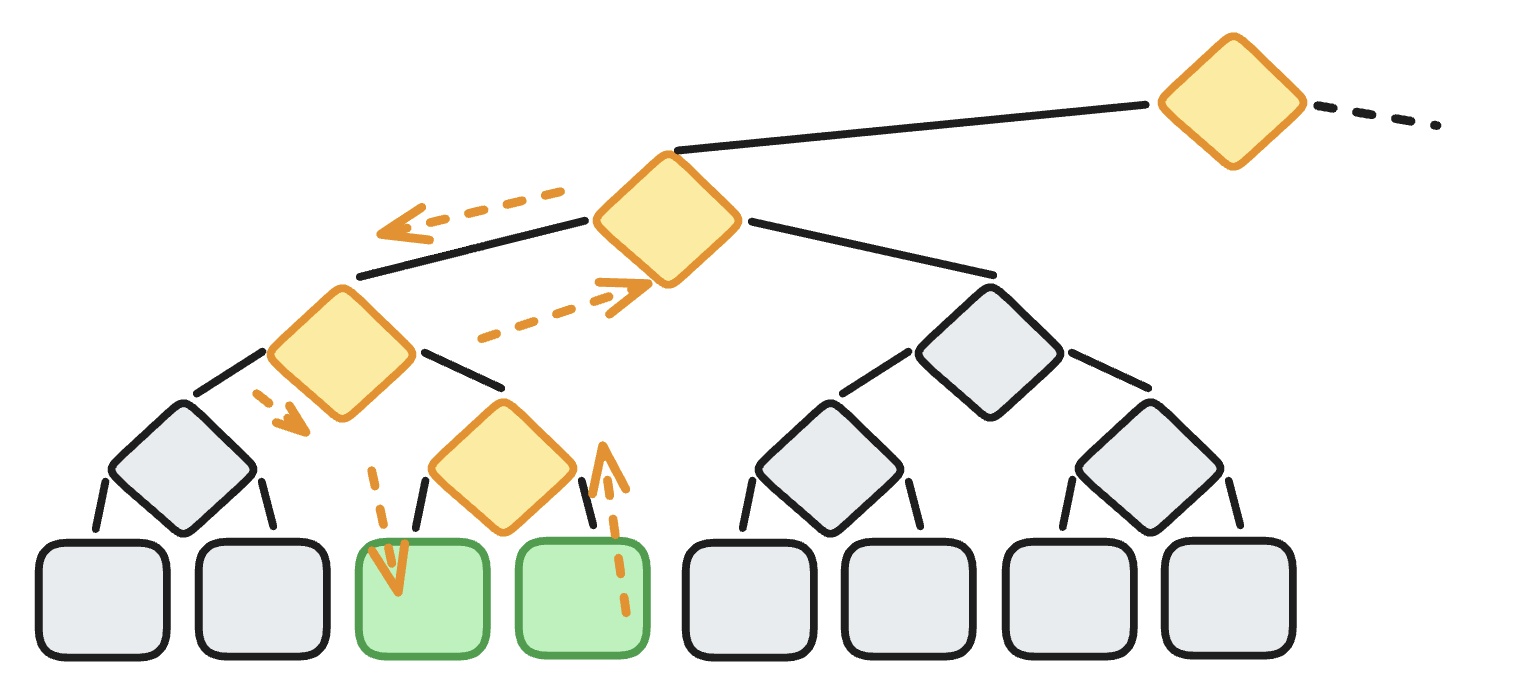
For our overlaid pending updates we use a map of list indices to values. When a value is updated, it gets inserted into this map. Multiple updates of the same index are supported by looking up the pending update in the map and replacing it with the latest update. Updates get applied in bulk when the caller requires it, by walking down the tree recursively and building a new tree with the updates grafted onto the unmodified parts of the existing tree. To do this efficiently, it's easiest if the pending updates are stored in an ordered map. This allows us to determine whether there are pending updates for a certain range (subtree) and to reuse that whole subtree if there are not. The default map is VecMap (essentially a Vec<Option<T>>) although Milhouse also supports BTreeMap. Experimenting with more map types could be an avenue for further optimization.
In the diagram above, indices 2 and 3 are updated (green), so the algorithm creates a new internal node as the parent of 2 & 3 (yellow). It then creates new parent nodes ascending the tree (yellow) while grafting in the unmodified subtrees (grey).
To dive deeper, check out the source for with_updates_leaves:
https://github.com/sigp/milhouse/blob/e838fd875d1bb7cec942741ca8c7c6d1a1bd3d9c/src/tree.rs#L157-L236
Rebasing
Another interesting algorithm in the Milhouse codebase is the one for rebasing. When loading states from disk Lighthouse is forced to create all-new trees for the data being loaded. Rebasing is the process by which these trees are de-duplicated with respect to existing trees already held in memory (e.g. the finalized state). The rebase algorithm for Lists and Vectors takes two trees as inputs and creates a new tree that is equivalent to the 2nd tree, but reuses identical subtrees from the 1st tree, thus reducing overall memory usage.
The implementation uses a recursive tree traversal which eventually compares the values at the leaves and propagates an "action" to take based on that comparison. For example, if two trees contain all the same leaves, then the algorithm will propagate an "equal-replace" action starting at the leaves and moving up the tree. We use the observation that if the left and right child of a node are exactly equal, then that node itself is exactly equal and can be reused in the rebased tree.
The full details of the algorithm are within the rebase_on function here:
https://github.com/sigp/milhouse/blob/e838fd875d1bb7cec942741ca8c7c6d1a1bd3d9c/src/tree.rs#L264-L405
Testing
Milhouse is thoroughly tested by a suite of property tests. We generate test cases that apply Milhouse's supported operations in a random sequence using random data. We compare the results calculated by Milhouse to the expected result for each test. The expected behaviour of Milhouse's types is quite easy to specify in terms of operations on Rust's standard Vec type.
In addition to property testing, we also use fuzzers to stress-test Milhouse's functionality and ensure that it is crash-free and bug-free. The fuzzing harnesses in Milhouse use AFL+ to explore code paths based on test coverage.
We welcome improvements to Milhouse's code, particularly where those improvements remove the scope for errors and improve reliability.
Single-pass epoch processing
Our tree-states work is closely linked to our research on optimizing Ethereum's state transition function in a provably correct way. The higher cost of iteration using tree-states motivated us to optimize epoch processing into a single iteration (pass). You can read more about the project and the ongoing formal verification work in this thread:
https://ethresear.ch/t/formally-verified-optimised-epoch-processing/17359
How to run tree-states
Since 2022 Lighthouse has offered an experimental mode that includes two big features. Those are:
In-memory tree-states
The feature of this post, is to reduce RAM while keeping more states in memory. Since v5.2.0 it is enabled by default for all Lighthouse users. To run it, just update Lighthouse to a version greater than or equal to v5.2.0. No further action is required.
New storage layout with hierarchical state diffs
Run a consensus archive node with ~200GB space, compared to 2TB+ today. This feature is not yet in Lighthouse stable. To use it you must download an experimental release of Lighthouse from https://github.com/sigp/lighthouse/releases.
At the time of writing, the latest experimental release containing this feature can be found here.
This feature is close to ready and is coming soon™️ targeting Q3 2024.
WARNING: experimental - use at your own risk


